Obr. 1 Náčrt Michelsonova interferometru (a), Interferenční obrazec na obrazovce detektoru (b)L – zdroj monochromatického světla (laser),
Ppz – polopropustné zrcadlo (polo-zrcadlo),
Pz – pevné zrcadlo,
Zp – posuvné zrcadlo umožňující měření délky vlny světla,
D – Detektor, na němž se zobrazuje interference světla.

Paprsek světla se od zdroje L šíří k Ppz. Zde se jeho část odrazí a šíří se k D (odražený paprsek). Půlka zbývajícího paprsku (přímý paprsek) směřuje k Pz a druhá půlka (kolmý paprsek) směřuje k Zp. Na obou zrcadlech se paprsky odrážejí a vrací se k Ppz. Zde se lámou a šíří se k detektoru D. Jelikož každý ze tří paprsků prošel trasu různé délky, jejich vlny dopadají na detektor v různé fázi (někde se vzájemně podpoří, jinde se částečně nebo úplně vyruší), čím na obrazovce vzniká interferenční obrazec (Obr. 1b).

V průběhu staletí se názor na to co je světlo postupně měnil. Vlnovou teorii světla navrhl Hayghens v roce 1690. V roce 1704 Newton navrhl tzv. korpuskulární teorii, podle které světlo je proud korpuskulí (částic). Jeho teorie byla uznávaná až do devatenáctého století přesto, že Newton neřekl co ta korpuskule je, a s jeho teorii nebylo možné vysvětlit interferenční jevy. V roce 1803 Young publikoval svůj dvojštěrbinový experiment, který ilustruje interferenční jev. Tímto experimentem byla oživena vlnová teorie, která pak vládla po celé devatenácté století.

V dvacátém století názor na světlo je již ve znamení kvantové elektrodynamiky (QED). Světlo je považováno za proudění fotonů, čím se velkým obloukem vracíme k Newtonově korpuskulární teorii, ovšem s tím, že korpuskule dostala konkrétní obsah v podobě fotonu. Teorii světla podle QED zpřístupnil široké veřejnosti Feynman svou populární knihou Strange theory of light and matter vydanou v roce 1985 (český překlad [1],[2] – viz Odkazy).

Foton objevil Einstein v roce 1905, když se snažil vysvětlit jev zvaný fotoefekt. Foton je elementární částice světla, která se pohybuje rychlostí světla a má energii E = h × f, kde h je Planckova konstanta a f je frekvence světla, která se projevuje barvou světla. Foton nikdo „neviděl“, vnímáme ho jen při jeho dopadu na sítnici oka, nebo na detektor speciálních přístrojů. V povaze lidského myšlení je přiradit těmto neviditelným přírodním aktérům objekty, které dobře známe z každodenního života. Feynman přirovnává foton k hodinkám s jednou ručičkou, která se otáčí frekvencí f. Na Obr. 2 je foton, coby hodinky, zobrazen kolečkem s jednou ručičkou – vektorem. Budeme mu říkat vektor fotonu.

Obr. 2 Ilustrace funkce M-interferometru dráhovým integrálem  (michelson.exe)Ve Feynmanově pojetí lze projevy světla vysvětlit, když přijmeme následující postuláty.

• V rámci QED dokážeme vypočítat jen pravděpodobnost dopadu fotonu na určený bod prostoru (detektoru).
• Nevíme, jakou cestou letí foton mezi zdrojem a určeným bodem, proto při vyhodnocení pravděpodobnosti je třeba počítat se všemi možnými trasami mezi zdrojem a bodem dopadu.
• Při dopadu fotonu jeho vektor vykazuje jistý úhel natočení, jehož stupeň závisí na délce absolvované trasy. Pro vyhodnocení pravděpodobnosti je třeba vektorově sčítat vektory fotonu letícího po všech trasách. Vektorové sčítání znamená připojení začátku vektoru ke konci vektoru předešlé trasy (Obr. 2 – vektory). Tomuto sečtení se říká dráhový integrál.
• Délce sumárního vektoru (spojujícího začátek prvního vektoru s koncem posledního) se říká amplituda dráhového integrálu.
• Pravděpodobnost dopadu fotonu na určený bod je úměrná kvadrátu amplitudy.

K dráhovému integrálu nejvíc přispívá přímá dráha, a proto považujeme šíření světla po přímce. Výpočet pravděpodobnosti se tím zjednoduší a pohyb fotonu mezi dvěma klíčovými body můžeme považovat za pohyb po přímce. V M-interferometru se foton pohybuje třemi trasami:

1. Laser – polo-zrcadlo – detektor (modrá),
2. Laser – polo-zrcadlo – posuvné zrcadlo – polo-zrcadlo – detektor (červená),
3. Laser – polo-zrcadlo – pevné zrcadlo – polo-zrcadlo – detektor (zelená).

Sinusoida na rameni mezi laserem a polo-zrcadlem zachycuje šíření světla, jak se obvykle zobrazuje vlnovou teorií. Tato sinusoida je ovšem jenom jiné zobrazení rotujícího vektoru promítnutého a rozvinutého do směru šíření světla. Tím chceme naznačit, že výše uvedené postuláty dráhového integrálu nevyjadřují nic, co by se nedalo říci i vlnovou teorii. Dráhovým integrálem se světelné děje jenom graficky snáze zobrazují.

Nezávisle na tom jakou trasu foton prošel, na úseku mezi polo-zrcadlem a detektorem prochází po stejné trase a jeho trasa na Obr. 2 je vyznačena modře, červeně a zeleně. Stejnými barvami jsou zobrazeny i jeho vektory. Zbylé úseky tras fotonu jsou bílé.

Podle Obr. 2 je zřejmé, že rozdílnost drah fotonu spočívá jenom v rozdílné délce ramen interferometru pevného a posuvného zrcadla. Pro pravděpodobnost výskytu fotonu v daném bodě detektoru přesto rozhoduje amplituda sumárního vektoru mezi daným bodem a koncem červeného vektoru, která na Obr. 2 je zobrazena žlutě.

Na Obr. 2 je zobrazen také mikrometr, s kterým lze posuvné zrcadlo posouvat. Sinusoida ilustruje jeho stupnici. Posune-li se posuvné zrcadlo o délku d, pak dráha fotonu od polopropustného zrcadla k posuvnému zrcadlu a zpět naroste o délku 2×d. To znamená, že 1.5 period sinusoidy stupnice mikrometru představují 3 vlnové délky světla.

Obrazec pravděpodobnosti vykazuje periodicky se vyskytující maxima, byť by měl detektor jakoukoli šíři. Naproti tomu, interferenční obrazec (Obr. 1b) ukazuje klesající jas interferenčních kruhů se vzdáleností od centra obrazce. Příčina toho vězí v tom, že pravděpodobnost se týká jednoho fotonu, zatímco jas obrazu je určen množstvím dopadajících fotonů na daný bod detektoru. Toto množství N klesá podle jiné pravděpodobnostní zákonitost, která je závislá na konstrukci přístroje v němž se zdroj nachází. Výsledný jas je pak dán součinem pravděpodobnosti jednoho fotonu a N.

Polohu posuvného zrcadla lze měnit mikrometrem. Jeho stupnici zobrazuje vlnovka (sinusoida), jejíž vlnová délka odpovídá vlnové délce posuvu posuvného zrcadla. Délka vlny je pojem zavedený ve vlnové teorii a znamená vzdálenost dvou sousedních vrcholů vlnovky. Pojem vlnová délka se používá i v QED teorii, kde znamená délku fotonem proletěné dráhy za dobu jednoho cyklu (otočky) vektoru fotonu.

Obr. 3 Interferenční obrazce při různých polohách posuvného zrcadla(b) (michelson.exe)

• Na Obr. 3a je interferenční obrazec zobrazen v také poloze posuvného zrcadla, kdy je dobře vidět sčítání vektorů fotonu z jeho jednotlivých drah, a jejich sumární vektor.
• Na Obr. 3b jsou zobrazeny výsledky v také poloze posuvného zrcadla, kdy červený vektor ukazuje týmž směrem jako zelený, čímž vznikne nejdelší amplituda sumárního vektoru (žlutá). To znamená, že rozdíl úhlů otočení červeného a zeleného vektoru činí celistvý násobek 360°. Jinými slovy, délky drah, které foton absolvoval k pohyblivému resp. k pevnému zrcadlu a zpět k polo-zrcadlu, jsou rozdílné o celistvý násobek vlnové délky světla.
• Na Obr. 3c jsou zobrazeny výsledky v také poloze posuvného zrcadla, kdy červený vektor ukazuje proti směru zeleného (červená úsečka překrývá zelenou a žlutý sumární vektor překrývá modrou úsečku). To znamená, že rozdíl úhlů otočení červeného a zeleného vektoru činí lichý násobek 180°. Jinými slovy, délky drah, které foton absolvoval k pohyblivému resp. k pevnému zrcadlu a zpět k polo-zrcadlu, jsou rozdílné o lichý násobek poloviční vlnové délky světla.

V animačním programu dokážeme znázornit vektory fotonu, ale na obrazovce interferometru je nevidíme. Tam vidíme jenom interferenční obrazce, a z nich žádné údaje o vlnové délce světla nevyplývají. Posouváním zrcadla se tvar interferenčního obrazce mění, a jeho podoba se periodicky opakuje (program m-posuv.exe) Posunutím zrcadla o d se délka dráhy fotonu změní o 2×d. Napočítáme-li N opakování téže podoby interferenčního obrazce, pak z toho vyplývá, že vlnová délka světla je λ = 2×d/N.

V devatenáctém století převládal názor, že světlo se šíří vlněním éteru. Jenže co je to éter? To nikdo nevěděl a tak se navrhovaly různé hypotézy. Jedna z nich byla, že je to jakási stacionární látka v celém vesmíru. Každý objekt, který se v něm pohybuje, musí pociťovat určitý „éterový vítr“, který je tím silnější čím je rychlost objektu větší. Sluneční soustava jako celek se v éteru pohybuje rychlosti Vs. Jenže Země a na ní instalovaný interferometr se pohybuje kolem Slunce přibližně po kruhové dráze rychlostí Vz = 35 km/s. Podle Obr. 4 je zřejmé, že okamžitý rozdíl rychlosti V Země od rychlosti Vs Slunce se mění podle ročního období podle sinusoidy v mezích ±Vz. Hledal se optický přístroj, který by tento rozdíl rychlosti měřil s přesností větší než Vz/c, kde c = 300 000 km/sec je rychlost světla ve vakuu. Požadovaná přesnost tak byla ±Vz/c = ±35/300 000 ~ ±0.00001, což je extrémně malá hodnota.

V roce 1880 Michelson vyvinul interferometr, který pak zdokonaloval pomocí Morleye, a který převyšoval požadovanou přesnost. Přístroj se mohl také otáčet, takže daly se s ním pozorovat nejen „sezónní“, ale také „denní“ změny interferenčních obrazců. Poslední měření s tímto interferometrem se opakovaně konaly v Clevelandu v roce 1887.

Obr. 4 K vysvětlení éterového větruVýsledky měření byly záporné, jelikož žádné sezónní ani denní změny interferenčních obrazců nebyly pozorovány. S těmito výsledky Michelson dozajista byl zklamaný, jelikož záporný výsledek experimentu se vždy dá zpochybnit. Nelibě to nesli i další významní fyzikové. Zpochybňování existence éteru znamenalo ztrácení stacionární vztažné soustavy (pevného bodu) ve vesmíru, a to znamenalo zpochybňování také Newtonovy mechaniky. Proto vznikaly hypotézy jak zachránit éter a tím Newtonovu mechaniku.

K vysvětlení podstaty světla éteru nebylo třeba, jelikož Maxwell již v roce 1865, na základě svých rovnic, mohl konstatovat, že světlo je vlnění elektromagnetického pole. K vysvětlení záporného výsledku M-M experimentu Einstein v roce 1905 navrhl radikálně novou Speciální Teorii Relativity (STR), která nepotřebuje pevný bod ve vesmíru, protože všechno je relativní, kromě rychlosi světla. Newtonova mechanika je založena na principu invariantního času v každé vztažné soustavě nezávisle na tom, zda se tato pohybuje či nikoliv (každý člověk stárne v rychle jedoucím autě stejně jako doma v posteli). Naproti tomu STR vychází z principu, že invariantní je rychlost světla c ve vakuu v každé vztažné soustavě, pokud se tyto vzájemně pohybují rovnoměrně a přímočaře, byť rozdílnou rychlostí (inerciální soustavy). Tento princip vyplynul už i z Maxwellových rovnic, ze kterých lze pro rychlost světla ve vakuu odvodit rovnici c = 1/√(μ × ε), kde μ a ε jsou permeabilita resp. permitivita vakua, což jsou konstanty Maxwellových rovnic a jsou nezávislé na rychlosti zdroje světla.

STR vede k podivuhodným výsledkům: dilatace času (zpomalení plynutí času) a kontrakce délek (zkrácení délek). Dilatace času znamená, že hodiny v rychlejší vztažné soustavě tikají pomaleji a to nejen atomové, ale i „biologické” – člověk v rychle jedoucím autě stárne pomaleji než doma v posteli.

Na následujícím příkladu ze „sportovního prostředí“ ukážeme, jak chápat relativitu času a délky v inerciálních vztažných soustavách.  Časoměřič naměří sprinterovi na 100 metrové trati, dejme tomu, čas T = 10 sec. Sprinterovy hodiny, které má atlet u sebe, však ukazují jen T* = 9 sec. Do seznamu rekordů se ovšem zapíše čas T, který ukazují hodiny časoměřiče.

Při sportovních utkáních se měří ledaco. Měří se také délka kroku sprintéra pomocí laserového měřiče délky, který je instalován poblíž běžecké dráhy, a zaznamenává maximální rozpětí palce levého a pravého chodidla atleta při běhu. Takto naměřená délka kroku, dejme tomu, je L = 150 cm. Sprintér má u sebe také laserový měřič délky, s nímž také měří délku svého kroku jako maximální rozpětí palce levého a pravého chodidla. Sprinterův krokoměr ovšem ukazuje délku kroku L* = 166.6 cm. Nicméně, do statistiky se zapíše délka kroku L naměřená „klidovým” měřičem délky.

Nelze tvrdit, že údaje naměřená hodinami časoměřičů a laserovým měřičem délky instalovaným podél závodní dráhy jsou správné a údaje naměřené sprinterovými přístroji jsou chybné. Časové a délkové údaje jsou relativní hodnoty a mají platnost v rámci své vztažné soustavy. Dilatace času, kontrakce délek a další relativní pojmy fyziky, jako hmotnost, současnost atd., jsou závislé na faktoru F = (1–(v/c)² )^1/2, kde v je rychlost vztažné soustavy (sprintéra) vzhledem ke „klidové” soustavě (časoměřiče). Jelikož 0 < F < 1, v pohybující se soustavě naměřený čas T* se v klidové soustavě prodlouží na delší T = T* / F, a délka L* se zkrátí na L = L* × F. Kontrakce délek se ovšem týká jen těch délek, které jsou ve směru rychlosti. Délky v kolmém směru zůstávají beze změny. V každodenním životě dilataci času a kontrakci délek nepozorujeme, jelikož rychlost v je vzhledem rychlosti světla zanedbatelně malá, a tak faktor F je prakticky F = 1.

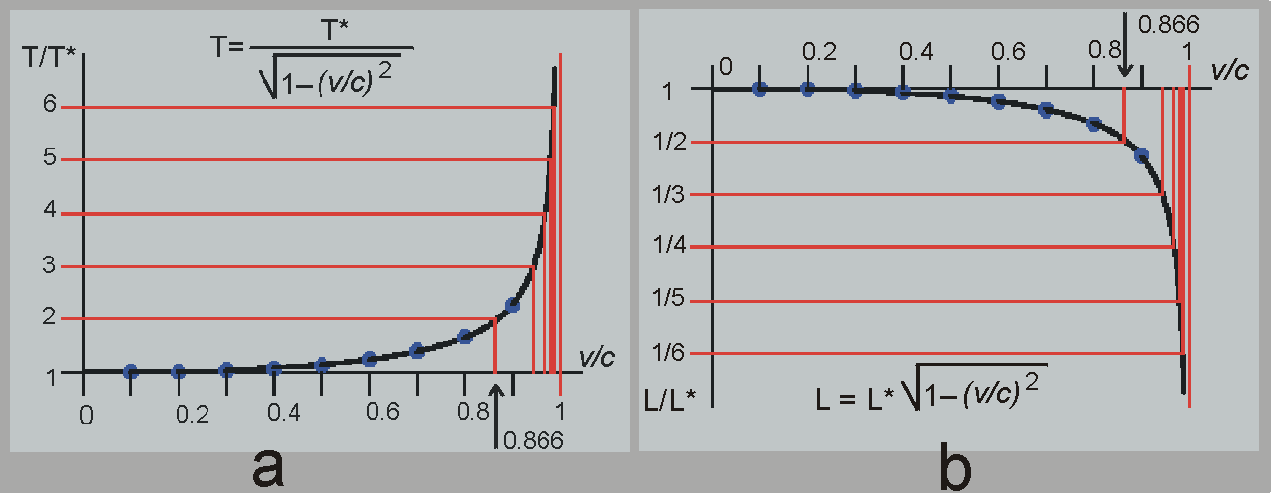
Dilatace času (a), kontrakce délky (b)  Kdyby pirát silnic svou rychlou jízdou chtěl stárnout dvakrát pomaleji, než stárnou diváci stojící opodál silnice (jeho čas T* plyne dvakrát pomaleji než čas diváků T), musel by jet rychlostí  v=  0.866×300000 = 259800 km/h. Na fotografii jeho vozu na parkovišti má auto délku L*. Na snímcích pořízených diváky během zběsilé jízdy by auto mělo poloviční délku L = 0.5×L*.

Výše uvedená rovnice faktoru F = (1–(v/c)² )^1/2 vyplývá z principu invariantnosti rychlosti světla. K její odvození vystačíme se znalostí středoškolské matematiky, konkrétněji, se znalostí Pythagorovy věty ([7] – viz Odkazy).

Důsledky STR ilustruje Obr. 5. M-interferometr, který je instalován na korbě nákladního auta. Jeho vztažná soustava je zobrazena osami y*, z*. Na silnici je umístěn také laser L, jehož vztažnou soustavu představují osy y, z. Stopa fotonu od laseru k polopropustnému zrcadlu Ppz je zelená. Stopa od Ppz k posuvnému zrcadlu Zp a odtud k detektoru D je bílá. Stopa od Ppz k pevnému zrcadlu Pz a odtud k detektoru D je modrá. Bíle jsou vyznačeny okamžité polohy zrcadel, kdy na ně dopadl foton.

Obr.5 M-interferometr v pohybu rychlém (a), pomalém (b), v klidu (c) (str-ilustrace.exe)Pokud automobil stojí, děje v M-interferometru jsou zobrazeny na Obr, 5c. Pohybuje-li se automobil stálou rychlostí, obraz dějů se změní na Obr. 5a,b. Modrá stopa v úseku Ppz – Pz se zkrátila, což odpovídá kontrakce délky ramena pevného zrcadla Pz, které je ve směru rychlosti auta. Délka ramena posuvného zrcadla Pzp se nezměnila, jelikož toto rameno je kolmé ke směru rychlosti. Zato však dráha fotonu k posuvnému zrcadlu Pzp a odtud k detektoru D doznala podstatných změn. Červená úsečka ukazuje, že foton odražený od Pzp je již na cestě k detektoru D, ale foton ještě nedorazil k pevnému zrcadlu Pz. Délka červené úsečky je mírou dilatace času, která se zmenšuje s nižší rychlosti auta, jak to ilustrují Obr. 5a,b.

Pozorovatel sedící na automobilu vidí dráhu fotonu na obrazovce jako na Obr.5c, bez ohledu na to zda auto jede, nebo stojí. Zato však, pozorovatel ze silnice vidí dráhy fotonu a interferenční obrazce podstatně odlišné v závislosti na rychlosti auta. Všechny předměty včetně interferenčního obrazce zeštíhlily ve směru rychlosti. Je to všechno ve shodě s M-M experimentem. Tam se M-interferometr spolu s Michelsonem a Morleyem vezli na Zemi a Slunce bylo zdrojem světla. Interferenční obrazec se neměnil podobně, jako se nemění pozorovateli vezoucím se v autě (Obr. 5c). Pozorovatel odněkud v Galaxii by viděl střídavě se měnící obrazce, jako na Obr. 5 a resp. Obr. 5b, v souladu s měnící se rychlosti Země vzhledem k Slunci podle sinusoidy (Obr. 4b).

Michelson byl v roce 1907 poctěn Nobelovou cenou za jeho přesné optické přístroje a výzkum prováděný pomocí nich. Einstein obdržel Nobelovou cenu v roce 1921 za příspěvek k teoretické fyzice, zejména za objev zákonitostí fotoelektrického jevu.